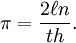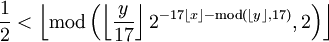bildirgec.org

Dalış sporu (scuba veya serbest dalış) ya da sörf ile uğraşanlar bilirler, kullanılan elbiselerin kurutulması ve saklanması ile ilgili sıkıntılar vardır. Haftasonu dalışa gidersiniz, gece gelir elbisenizi yıkar yatarsınız. Evde bir türlü kurumaz, hele de kışın. Uzun sürse de sonunda kuru ama bu sefer de koku yapar. Arada bir sabunlu suyla yıkamak lazımdır ama her sabun her kimsayal kullanılmaz bu elbiselerin yıkanmasında.

Hangair

İşte bu sorunlar çare bir ürün: HangAir Aslında üzerinde güçlü bir fan bulunan askıdan başka birşey olmayan bu ürünün iddiası, daha kısa sürede (%70’e varan) kuruma ve kokusuz bir elbise.
50 dolar civarı bir ücretle internetten alınabilir ama Türkiye’de dağıtıcısı var mı bulamadım.

Hafif camiasında bir yeniliğe imza atmanın mutluluğunu yaşıyorum. Siz şu anda bu yazıyı okurken, yazının konusu oluşturan müzik parçasını da size dinletebiliyorum. Bu hizmeti size ulaştırabilmemdeki en büyük kolaylığı bana, parçanın bestecisi olan John Cage sağlamaktadır.
Amerikalı besteci John Milton Cage Jr. (1912–1992) enstrumanların alışılmışın dışında kullanımları, elektronik müzik ve rastlantısal müzik (chance music-en uygun Türkçe karşılık bu gibi geldi) konularında bir öncüymüş. Aynı zamanda filozof ve yazar olan John Cage 1952 yılında dört dakika otuzüç saniyelik bir beste yapmış. Bestenin adı da 4’33”. (Daha önce hafif’te adı geçmiş ve -şu anda bağlantı çalışmasa da- bağlantı verilmiş ama kendine ait bir yazıyı hakettiğini düşündüm bu bestenin.)

John Cage

İlk olarak piyano ile icra edilse de beste aslında her türlü enstrumanla icra edilebilir bir yapıdadır. Çünkü tamamıyla sessizlikten oluşan üç bölümden ibarettir. Bu üç parçanın uzunluğu icra edenin kendi kararına bırakılmıştır. Aslında parçanın tamamının uzunluğu da icra edenin kendi keyfine kalmıştır. Besteleri kendi egosundan etkilenmesin diye beste yaparken tarot kartlarına baktığı yönünde söylentiler olan biri için bu yaklaşım oldukça normal.

http://www9.gazetevatan.com/haberdetay.asp?tarih=08.08.2007&Newsid=131440&Categoryid=7

Matematik ile ilgili ilginç bir–ikikeşif yazısı yazıp epeyi yorum ve “tutma” aldıktan (bu nasıl söylenir ya) sonra en az onlar kadar ilginç olduğunu düşündüğüm başka bir keşif yazısı yazdım. Bu yazı sadece bir yorum ve beş tutma (bunu yazdığımdaki durum) ile kaldığında bu konu üstüne biraz kafa yordum. Eee, hafif ahalisiyiz, sadece kafa yormadım wikipedia‘yı biraz bu konuda eşeledim. Karşıma tam da aradığım şey çıktı. Warnock Çıkmazı ya da Warnock’s Dilemma.

Pi’nin basamaklarında yinelenen sayılar ve kendini çizdiren formül yazılarından anlaşılıyor ki hafif camiasında matematiğe, matematik dünyasındaki ilginçliklere benim gibi ilgi duyan az insan yokmuş. Buyrun o zaman; yine konumuz matematik.

Yanyana çakılmış eşit genişlikte tahta parçalarından oluşan ahşap bir masa düşünün. Bu masanın üzerine, belirli bir yükseklikten bir iğne bırakın. İğne tahtalar arasındaki çizgileri kesen bir pozisyonda mı düştü, yoksa hiçbir çizgiye dokunmuyor mu? Bir tane daha atın. Bu sefer ne oldu? İki durumdan birinin olma olasılığı nelere bağlı? Bu deney doğa bilimcisi, matematikçi Georges-Louis Leclerc, Comte de Buffon‘un aklına 18. yüzyılda takılmış. Kendisi olasılık teorisi konularına türev ve integrali sokmuş ve olasılık teorisi üzerine oldukça fazla kafa yormuş bir aydınlanma dönemi bilim adamı. Buffon’dan daha sonra biraz bahsedeceğiz; önce şu deneye dönelim. Buffon’un İğne Problemi: “l” uzunluğunda bir iğne, aralarında “t” birim uzaklık olan paralel çizgilerden oluşan bir zemine düştüğünde çizgilerden birini kesme olasılığı nedir? Birçoğumuz metematikçi değiliz ama yine de şöyle biraz kafa yorarsak bu problem bizi ilginç bir noktaya götürüyor.

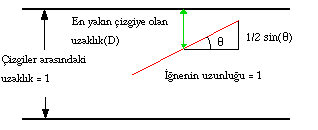
Durumun gösterimi

İğnenin çizgileri kesme olasılığı iğnenin orta noktasının en yakın çizgiye olan uzaklığı ve iğnenin çizgilerle oluşturduğu açıya bağlıdır. Çok sayıda iğne attığınızda kaç iğnenin çizgileri keseceğini de hesaplamak isterseniz, biraz türev biraz integral (çözüm detayı için şuraya bakılabilir) sonucunda ortaya iğne uzunluğu, çizgiler arasındaki uzaklık, atılan toplam iğne sayısı, çizgileri kesen iğne sayısı ve bizim ünlü pi sayısını içeren bir sonuç formülü çıkar (pi’nin bağlantısı açıdan kaynaklanır). İğnenin uzunluğunu ve çizgiler arasındaki uzaklığı bildiğinizde, pi’yi hesaplamak için geriye çizgilere doğru çok sayıda iğne atıp kaçının çizgileri kestiğine göz atmak kalır. (n adet iğne bırakırsak ve h kadarı çizgileri keserse)

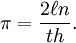
pi hesaplamanın bir yolu

Evet, bu olasılık probleminin ilginç yanı bu: pi sayısının değerini bulmanın olasılık kullanılan bir yöntemi olması.

Geçen hafta Pi’nin basamakları arasında saklı yinelenen rakamlardan söz etmiştik. Bu hafta da matematik dünyasından çarpıcı bir formüle göz atacağız.
Toronto Üniversitesi Bilgisayar Bilimleri Bölümü’nden Jeff Tupper, kendi geliştirdiği GrafEq isimli formül grafiklerinin çiziminde kullanılan uygulama ile ilgili yöntemlerden bahsettiği makalesinde, resimdeki eşitsizlikten sözeder.

Tupper’ın eşitsizliği

Bu eşitsizlikte, alt kısmı köşeli parantezler, matematik ve programcılıktaki floor fonksiyonunu temsil etmekte (bilmeyenler için: tamsayı olmayan bir sayı için, o sayıdan küçük en büyük tam sayıyı döndüren fonksiyon). mod ise, moduloyu yani bir bölme işleminde kalanı döndüren fonksiyonu temsil etmekte.
Eşitsizliği 0<x<<106 ve n<y<n+17 aralıkları ve n = 960939379918958884971672962127852754715004339660129306651
505519271702802395266424689642842174350718121267153782770
623355993237280874144307891325963941337723487857735749823
926629715517173716995165232890538221612403238855866184013
235585136048828693337902491454229288667081096184496091705
183454067827731551705405381627380967602565625016981482083
418783163849115590225610003652351370343874461848378737238
198224849863465033159410054974700593138339226497249461751
545728366702369745461014655997933798537483143786841806593
422227898388722980000748404719 (biliyorum şaka gibi bir sayı ama napalım :o) ) için çizdirdiğinizde ortaya çıkan monokrom bitmap görüntü formülün kendisi olur. Yani formül aslında kendisini çizdirmektedir.

Sonuçta ortaya çıkan imaj

Formulün JavaScript ile gerçeklenmiş halini ve bu gerçeklemenin çizilişini izlemek için şurayabakabilirsiniz.

Pi’de yinelenen rakamlar

Resimde de görüldüğü üzere Pi sayısının ilk birkaç yüz basamağında iki veya üçer kez yinelenen bazı rakamlar vardır. Ancak 762. basamakta başlayan ve altı adet 9’un oluşturduğu seri gerçekten şaşıtıcıdır. Bu altılı yineleme ilk olması açısından o kadar ilginçtir ki (bundan önce dörtlü veya beşli bir yineleme yoktur) bir isim verilmeyi ve bu isimle anılmayı hakeder. Yinelemeye ünlü fizikçi Richard Feynman‘ın adı verilmiş ve Feynman Noktası olarak adlandırılmıştır. Bunun nedeni ise şudur: Feynman birgün ders anlatırken öğrencilerine Pi sayısını bu yinelemeye kadar ezberlemek istediğini, çünkü böyle yaptığında ezberin sonuna gelip “dokuz dokuz dokuz dokuz ve böyle sürüp gider…” diyebileceğini söylemiştir. Buradaki gönderme insanların Pi sayısının bir basamakan sonra yinelemeye girebileceği inancına yapılan bir göndermedir.
Seçilen herhangi bir irrasyonel sayının basamakları içinde yinelenen altı tane dokuzun bulunma olasılığının yüzde 0.08 olmasıdır. İlginç olan Pi sayısının basamakları içinde altı adetten oluşan bir sonraki yinelemenin de (193.034ncü basamaktaki) dokuzlardan oluşuyor olmasıdır. Hatta daha da ilginç olanı Pi’nin ilk dört milyon basamağında bu altı dokuzdan oluşan yinelemeden 8 adet mevcuttur. Şu sayfadaki Pi basamaklarını bulma aracı ile yinelemeleri kontrol edebilirsiniz.
Siz de Feynman gibi Pi’nin basamaklarını ezberlemek isterseniz Piphilogy‘den faydalanabilirsiniz. Ya da daha farklı yöntemler kullanabilirsiniz.
Bu arada basamak ezberlemekten bahsedip şu an için geçerli olan rekoru belirtmeden olmayacak: son rekor 3 Ekim 2006’da Akira Haraguchi tarafından 100,000 basamakla kırılmıştır. Daha önceki tüm rekorlar için…

Diyelim Google Desktop kullanıyorsunuz. Ve diyelim diskinizdeki C: sürücünüzde (drive) yer sıkıntısı başgöstermeye başladı. Partition Magic tarzı birşeyler kullanarak diğer sürücülerden yer alıp C: sürücünüze biraz daha alan kattınız. Hatta bunu birkaç kez yaptınız ama -artık ne nedenleyse :o)- yer sıkıntısı devam ediyor. WinDirStat veya benzeri bir uygulamayla dizinlerin ve dosyaların kapladıkları alanları kontrol ettiniz. Bir de baktınız ki Google Desktop’ın indeks dosyaları almış başını yürümüş. (Google Desktop indekslerini varsayılan (default) ayar olarak C:Documents and SettingsUSERNAMELocal SettingsApplication DataGoogleGoogle Desktop dizini içinde tutuyor.) Bakınıyorsunuz, “bunları nasıl etsem de başka dizinlere alsa”m diye. İşte Google‘da arama yaptığınızda o zaman karşınıza bu yazı çıkacak ve siz TweakGDS ile tanışacaksınız.

TweakGDS kullanıcı arayüzü

TweakGDS, kendi deyimiyle Google Desktop’ın dökümante edilmemiş özelliklerini değiştirmenizi sağlıyor. En önemlisi de indeks dosyaşarının yerini değiştirebiliyor olmanız. İlk açılışta önemli bir uyarı ile karşılaşıyorsunuz; yapacağınız işlemlerin tehlike içerdiği ve herhangi bir kayıp yaşarsanız uygulamayı geliştirenlerin sorumlu olmadıkları vs. yazıyor. Ben de aynı şeyi söyleyeyim; evet aslında yapılan işlem çok da “tereyağından kıl çeker” gibi bir işlem değil. Kullanıp kullanmamya kendiniz karar verin. Ama ben denedim, sıkıntı yaşamadım. Benzer bir sıkıntısınız varsa bir göz atmakta fayda var.

Geçenlerde aklıma düştü, youTube ve benzeri birkaç video sitesinde 80’li yıllarda Metin Akpınar ve Zeki Alasya’nın oynadığı aşı ve kdv fişi kampanyalarının skeçlerini aradım. Hani hatırlarsınız “eşeğü hemen aşulatacağum” veya “çocuğa aşı olmaaaz zeytune zeytune” cümlelerini. Bu ikili ile ilgili filmleri, kabareleri ve birkaç reklam gibi birçok video var ama bu trt skeçlerine rastlayamadım. Bir yerlerde bu skeçlerin videolarının varlığından haberdar olanınız var mıdır?

bunu bile yayınladılar

blog kardeşliğini ya da bloglar alemini takip edenler bilir, türkiye’deki bloglar arasında hatırı sayılır miktarda yemek ve yemekle ilgili blog vardır. bazıları yemek tarifleri verir, bazıları tarif denemelerini paylaşır, bazıları ise gezip gördüklerini, yediklerini yazar. gelelim konumuza. efendim gurme.net alanadı altında yeralan site bu bahsettiğim türkçe yiyecek/içecek sitelerinin içeriklerini bu sitelerin sahipleri olmaksızın alıp görüntülüyor. bu olayı buraya taşımazdım normalde ama araklama olayı hakikaten çok acayip noktalarda. anladığım kadarıyla içerikler rss kaynakları sayesinde programatik olarak (kimsenin süzgecinden geçmeden) alınıp otomatik biçimde gurme.net’te görüntüleniyor. bunu anlamamız ise şöyle oldu: içerikleri alınan site sahipleri bu kişilerle hiçbir şekilde iletişim kuramadıklarından farklı bir protesto yoluna gidip sitelerine gurme.net’i kötüleyen hatta hakaret eden postlar yazdılar. ve gurme.net sitesi bunları da yayınladı. iş o kadar garip ki, en azından haftada bir girip yanlış giden birşey var mı diye bakmıyorlar bile. nasıl olsa içerik otomatik olarak oluşuyor ve google reklamları yayınlanıyor ya, gerisi gurme.net sahiplerinin umurunda değil. aslında belki de yasal yollardan mücadele edilebilir ama yasalarımızın bu konuda çok da yeterli olmayabileceğini düşünüyorum.

şimdi bu bildiriden dolayı sizler de bu siteye girip olana bitene bakacaksınız. artık bir gerçek olan bildirgeç etkisinden dolayı ziyaretçi sayıları tavana vuracak belki ama yapacak birşey yok. ayrıca olayın tam da bildirgeçlik bir bildiri olduğunu düşünüyorum.